机器学习入门笔记08

数据预处理

系列文章

数据预处理

非数值类型数据处理

哑变量处理

哑变量也称虚拟变量，通常取值为 0 或 1 。例如，将“性别”取值“男”或“女”处理为 0 或 1 ，以供模型处理。

可以使用 Pandas 库的 get_dummies() 函数处理哑变量：

df01 = pd.DataFrame({'gender': ['male', 'female', 'male'],
                     'salary': [3000, 2400, 3200]})
df01 = pd.get_dummies(df01, columns=['gender'])
df01
salarygender_femalegender_male
0300001
1240010
2320001

得到的结果被拆分为两列。由于这两列数据存在多重共线性，因此可以丢弃一列：

df01 = df01.drop(columns='gender_male')
df01 = df01.rename(columns={'gender_female': 'gender'})
df01
salarygender
030000
124001
232000

这样就得到了最终的结果。

编号处理

对于多个值的情况，还可以使用编号的方式将文本内容转换成数字。这种方式需要使用Scikit-Learn 中的 LabelEncoder 类：

df02 = pd.DataFrame({'zone': ['A', 'C', 'A', 'B', 'C', 'C'],
                     'id': [1, 2, 3, 4, 5, 6]})
from sklearn.preprocessing import LabelEncoder
label = LabelEncoder().fit_transform(df02['zone'])
label
array([0, 2, 0, 1, 2, 2])

接着只需要用得到的结果替换原始列即可。

哑变量和编号处理这两种方式都可以将非数值数据转换成数值数据，优点是可以作为特征变量参与预测，缺点是得到的数值没有实际意义，如果将这部分数值用于计算可能会发生问题。不过对于树模型来说一般不会造成什么影响。

除此之外，在分类不多，且分类名称明确的情况下，还可以使用 DataFrame 对象的 .replace() 或 .map() 方法，前者替换特定内容；后者对每个值进行特定操作，也可以实现特定的效果：

np.all(
    df02['zone'].replace({'A': 1, 'B': 2, 'C': 3}) ==
    df02['zone'].map({'A': 1, 'B': 2, 'C': 3}))
True

不过这种方式在处理未知的列时，可能还需要提前使用 .value_counts() 方法查看列中都存在哪些值。

正常化与标准化

去除异常值

假设要处理如下的数据：

df03 = pd.DataFrame({'salary': [31, 40, 27, 109, 33, 37],
                     'price': [15, 18, 31, 22, 13, 20],
                     'amount': [43, 71, 65, 39, 6, 54]})

可以发现数据中包含了部分过于悬殊的数值。这些数值有可能会给模型造成一定的污染，需要将其去除。

对于大量数据肯定不能人工去除，以下是两种检测异常值的思路：

利用箱体图观察

箱体图(box plot)是一种用于显示一组数据分散情况的统计图，可以通过设定标准将数值识别为异常值。

下图表达了箱体图的概念：

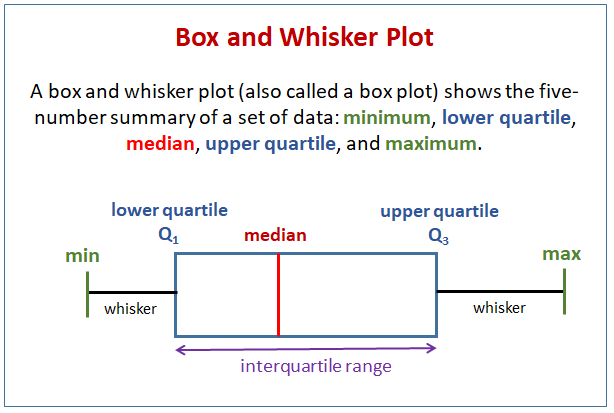
图片来源：https://www.onlinemathlearning.com/box-plot.html

将数据的下四分位记为 \\( Q_1 \\) ，上四分位记为 \\( Q_3 \\) ，上四分位和下四分位的差值记为 \\( \text{IQR} \\) ；箱体上界为 \\( Q_3 + 1.5 \times \text{IQR} \\) ，下界为 \\( Q_1 - 1.5 \times \text{IQR} \\) ，即为正常值的范围。

可以直接调用 DataFrame 的 .boxplot() 方法绘制箱体图：

df03.boxplot()
<AxesSubplot:>

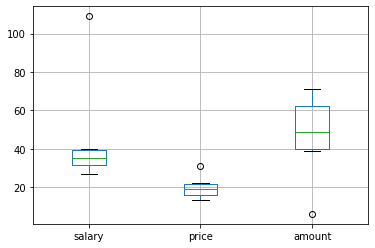
可以看到每个数据各有一个异常值。

利用标准差检验

当数据服从标准正态分布时，99% 的数据与均值的距离在 3 个标准差内，95% 的数字与均值的距离在 2 个标准差内。

在不用太严格的情况下，将阈值设定为 2 个标准差，当数据与均值的距离超出该阈值，即可认为它是异常值。

根据标准差检验异常值的代码如下：

df_abnormal = pd.DataFrame()
for i in df03.columns:
    z = (df03[i] - df03[i].mean()) / df03[i].std()
    df_abnormal[i] = abs(z) > 2
df_abnormal
salarypriceamount
0FalseFalseFalse
1FalseFalseFalse
2FalseFalseFalse
3TrueFalseFalse
4FalseFalseFalse
5FalseFalseFalse

其中第三行对每列数据实行 Z-score 标准化，具体的内容接下来会介绍。

得到的结果包含布尔值，可以根据结果剔除或修改含有异常值的数据。

数据标准化

在介绍K近邻算法时提到过数据标准化（数据归一化），主要目的是消除不同特征变量量纲级别相差过大造成的不利影响。

min-max标准化

min-max标准化(Min-Max Normalization)也称离差标准化，它利用原始数据的最大值和最小值把原始数据转换到 \\( [0,1] \\) 区间内，转换公式为：

\\[ x^*=\frac {x-\min}{\max-\min} \\]

其中 \\( x \\) 和 \\( x^* \\) 分别为转换前和转换后的值，\\( \max \\) 和 \\( \min \\) 为原始数据的最大值和最小值。

对于以下数据：

df04 = pd.DataFrame({'salt content': [1.5, 0.37, 1.22, 3.07, 0.55, 0.6],
                     'starch content': [31, 192, 60, 63, 88, 15]})

使用 Scikit-Learn 对以上数据用min-max标准化处理的方法为：

from sklearn.preprocessing import MinMaxScaler
X = MinMaxScaler().fit_transform(df04)
X
array([[0.41851852, 0.09039548], [0. , 1. ], [0.31481481, 0.25423729], [1. , 0.27118644], [0.06666667, 0.41242938], [0.08518519, 0. ]])

得到的结果都包含在 0~1 内。

Z-score标准化

Z-score 标准化也称均值归一化，通过原始数据的均值(mean)和标准差(standard deviation)对数据执行标准化处理。

该方式标准化后的数据符合标准正态分布，即均值为 0 ，标准差为 1 。它所使用的转换公式如下：

\\[ x^* = \frac {x-\text{mean}}{\text{std}} \\]

其中 \\( \text{mean} \\) 和 \\( \text{std} \\) 为原始数据的均值和标准差。

使用代码对数据 Z-score 标准化处理的代码与 min-max 标准化很类似：

from sklearn.preprocessing import StandardScaler
X = StandardScaler().fit_transform(df04)
X
array([[ 3.06816139e-01, -7.63757555e-01], [-9.24079378e-01, 2.04152685e+00], [ 1.81548011e-03, -2.58457880e-01], [ 2.01699841e+00, -2.06185500e-01], [-7.28007525e-01, 2.29417669e-01], [-6.73543122e-01, -1.04254358e+00]])

总之，不仅仅是K近邻算法，还有许多基于距离的算法也受到量纲的影响，需要提取对数据进行标准化处理。

数据分箱与特征筛选

数据分箱

数据分箱就是将一个连续变量离散化，可分为等宽分箱与等深分箱：

可以简单地用 Pandas 的 cut 函数执行等宽分箱：

boxes = pd.cut(X['EstimatedSalary'], 3)
boxes
0 (14865.0, 60000.0] 1 (14865.0, 60000.0] 2 (14865.0, 60000.0] 3 (14865.0, 60000.0] 4 (60000.0, 105000.0] ... 395 (14865.0, 60000.0] 396 (14865.0, 60000.0] 397 (14865.0, 60000.0] 398 (14865.0, 60000.0] 399 (14865.0, 60000.0] Name: EstimatedSalary, Length: 400, dtype: category Categories (3, interval[float64, right]): [(14865.0, 60000.0] < (60000.0, 105000.0] < (105000.0, 150000.0]]

利用得到的结果，可以通过分组获取每个分箱的样本数：

X['EstimatedSalary'].groupby(boxes).count()
EstimatedSalary (14865.0, 60000.0] 174 (60000.0, 105000.0] 160 (105000.0, 150000.0] 66 Name: EstimatedSalary, dtype: int64

分箱的主要目的是为接下来介绍的特征值筛选作准备。

特征筛选

构造一个模型可能需要一些特征变量，但有时数据提供的特征变量可能达到几十个，这时不可能将所有的特征变量都用于训练，需要筛选出一些典型的特征变量。

WOE值

WOE值即证据权重(Weight of Evidence)，反应了某一变量的特征区分度。

要计算一个变量的WOE值，需要先对该变量分箱处理，分箱后的第 \\( i \\) 个分箱内数据的WOE值的计算公式为：

\\[ \text{WOE}_i = \ln \left(\frac{P_{y_i}}{P_{n_i}}\right) \quad \text{where} \quad P_{y_i} = \frac{y_i}{y_T}, P_{n_i} = \frac{n_i}{n_T} \\]

\\( P_{y_i} \\) 是第 \\( i \\) 个分箱中目标变量取值为 1 的个体占整个样本中所有目标变量取值为 1 的个体比例，\\( P_{n_i} \\) 是取值为 0 的个体占比。

依照定义，可以对以上公式简单变换：

\\[ \text{WOE}_i = \ln \left(\frac{P_{y_i}}{P_{n_i}}\right) = \ln \left(\frac{y_i}{n_i}\right) - \ln\left(\frac{y_T}{n_T}\right) \\]

变换后，WOE值也可以理解为：分箱后第 \\( i \\) 个分箱中取值为 1 与取值为 0 的比值与整体比值的差异。如果这个差异很大，就说明各个分箱的区分度很高，能够较好地分类。

如果各个分箱，即不管数据取值范围如何，这个差异都很小，那就说明该变量对分类没什么影响，该变量就不够有特征性了。

通过以下代码，分箱并初步检查变量对分类的影响：

boxes = pd.cut(X['EstimatedSalary'], 5)
cut_all = Y.groupby(boxes).count()
cut_y = Y.groupby(boxes).sum()
cut_n = cut_all - cut_y
pd.DataFrame({'all': cut_all, 'purchased': cut_y, 'not purchased': cut_n})
allpurchasednot purchased
EstimatedSalary
(14865.0, 42000.0]953956
(42000.0, 69000.0]104896
(69000.0, 96000.0]1253194
(96000.0, 123000.0]38308
(123000.0, 150000.0]38353

仅从该表中，也能看出变量对结果的影响。接下来利用上述公式计算WOE值：

pd.DataFrame({'all': cut_all,
              'WOE': np.log((cut_y / cut_y.sum()) /
                            (cut_n / cut_n.sum())) })
allWOE
EstimatedSalary
(14865.0, 42000.0]950.224441
(42000.0, 69000.0]104-1.898675
(69000.0, 96000.0]125-0.523076
(96000.0, 123000.0]381.907987
(123000.0, 150000.0]383.042967

IV值

IV值即信息量(Information Value)，能较好地反映特征变量的预测能力。特征变量对预测结果的作用越大，IV值就越高。

各个分箱的特征变量通过以下公式计算：

\\[ \text{IV}_i = (p_{y_i} - p_{n_i}) \text{WOE}_i \\]

其中 \\( \text{IV}_i \\) 为一个特征变量第 \\( i \\) 个分箱的 \\( \text{IV} \\) 值。总的 \\( \text{IV} \\) 值就是每个分箱对应的值之和：

\\[ \text{IV} = \sum_i^n \text{IV}_i \\]

通过之前得到的 \\( \text{WOE} \\) 值，就可以方便地计算 \\( \text{IV} \\) 值：

IV = WOE * (cut_y / cut_y.sum() - cut_n / cut_n.sum())
IV.sum()
1.7433901102045861

处理多重共线性

对多元线性回归模型 \\( Y=k_0+k_1X_1+k_2X_2+\dots+k_nX_n \\) ，如果特征变量之间存在高度线性相关关系，则称为多重共线性(multicollinearity)，需要删去其中相关的变量。

除了完全共线性，模型可能还存在近似共线性：

\\[ a_1X_1+a_2X_2+\dots+a_nX_n+v=0 \\]

如果存在不全为 0 的 \\( a_i \\) ，其中 \\( v \\) 为随机误差项，则称特征变量之间存在近似共线性。

DataFrame 的 .corr() 方法可以立即检查各个特征变量之间的相关系数，从而判断变量之间是否具有多重共线性：

X.corr()
GNP.deflatorGNPUnemployedArmed.ForcesPopulationEmployed
GNP.deflator1.0000000.9915890.6206330.4647440.9791630.970899
GNP0.9915891.0000000.6042610.4464370.9910900.983552
Unemployed0.6206330.6042611.000000-0.1774210.6865520.502498
Armed.Forces0.4647440.446437-0.1774211.0000000.3644160.457307
Population0.9791630.9910900.6865520.3644161.0000000.960391
Employed0.9708990.9835520.5024980.4573070.9603911.000000

其中主对角线上是变量与自身的共线性，自然是 1 ；表中有许多变量之间的相关系数都超过了 0.95 ，可以认为它们之间有很强的共线性。

相关系数只是判断多重共线性的充分条件，可能会有遗漏的情况。为了更加严谨地判断是否存在多重共线性，可以使用方差膨胀系数(Variance Inflation Factor, VIF)法检验。

方差膨胀系数的计算公式如下：

\\[ \text{VIF}_i = \frac 1 {1- R_i^2} \\]

其中 \\( \text{VIF}_i \\) 是衡量自变量 \\( X_i \\) 与其它自变量的方差膨胀系数，\\( R_i^2 \\) 即 R-square 值。

一般来说，VIF 值大于 10 ，即说明变量存在一定的多重共线性；大于 100 时多重共线性就非常严重了。

Statsmodels 库提供了一种检验多重共线性的方法：

from statsmodels.stats.outliers_influence import variance_inflation_factor
vif = [variance_inflation_factor(X.values, X.columns.get_loc(i)) for i in X.columns]
vif
[7206.721374719253, 374.541409690173, 124.66977798735299, 49.836356753634455, 14317.230866912209, 17331.0914568944]

结果显示数据之间存在严重的多重共线性，需要删除一些特征变量，否则会使线性回归模型的预测能力下降。

过采样与欠采样

建立模型时可能遇到样本分类比例非常不均衡的情况，例如建立疾病预测模型时，未得病样本的比例应该远小于得病的。这部分失调的比例会浪费更多时间去拟合，导致测试结果不佳。

此时，可以选择过采样或欠采样的方式来弥补该缺点。

过采样

最简单的过采样方法是随机过采样，具体方式是在样本较少的分类中随机抽取一个旧样本拷贝为新样本，这样重复随机拷贝直到两个分类的样本数差不多为止。但是该方式会因为样本的重复，容易造成过拟合。

一种改进的方法是SMOTE法，即合成少数类过采样技术。这种方法根据样本不同将其分为两类，每次随机选取少数类中的一个样本，找到离该样本点最近的若干样本点，并在连线上随机取点生成新的样本点。

下图展示了这种过采样原理：

图片来自 medium.com ，具体地址未知

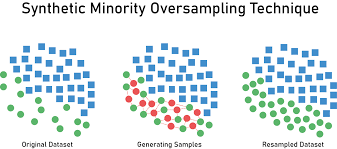
该方法可以看作让分类“变密”但不“变散”的一个过程

imbalanced-learn 是一个专门用于处理数据不均衡问题的工具库。可以通过 pip 直接安装，还可以通过克隆源代码的方式安装：

(sci) PS D:\MachineLearning\demo> git clone https://github.com/scikit-learn-contrib/imbalanced-learn.git
(sci) PS D:\MachineLearning\demo> cd imbalanced-learn
(sci) PS D:\MachineLearning\demo\imbalanced-learn> pip install .

使用以下代码可以执行随机过采样，同时统计过采样前后的结果；

from collections import Counter
print(Counter(Y))
from imblearn.over_sampling import RandomOverSampler
X_over, Y_over = RandomOverSampler(random_state=42).fit_resample(X, Y)
print(Counter(Y_over))
Counter({0: 257, 1: 143}) Counter({0: 257, 1: 257})

可以看到，过采样后两个分类的样本数一致。

类似地，以下的代码可以执行SMOTE法过采样：

from imblearn.over_sampling import SMOTE
X_over, Y_over = SMOTE(random_state=42).fit_resample(X, Y)

欠采样

与过采样相反的操作是欠采样。欠采样是直接舍弃大分类中的大部分样本，使两者样本数相等。因此欠采样的样本在搭建模型时可能导致欠拟合。

imbalanced-learn 库同样支持直接生成欠采样样本：

from imblearn.under_sampling import RandomUnderSampler
print(Counter(Y))
X_under, Y_under = RandomUnderSampler(random_state=42).fit_resample(X, Y)
print(Counter(Y_under))
Counter({0: 257, 1: 143}) Counter({0: 143, 1: 143})