机器学习入门笔记02

逻辑回归模型

系列文章

逻辑回归模型

算法原理

数学原理

不同于线性回归，逻辑回归主要用于预测离散的模型，例如一件事情是否会发生。

逻辑回归基于线性回归方程：

\\[ y = k_0 + k_1x_1 + k_2x_2 + \dots + k_nx_n + \dots \\]

线性回归方程的结果取值为 \\( (-\infty, +\infty) \\) ，而逻辑回归则借助 Sigmoid 函数将结果约束到概率取值范围 0~1 中，Sigmoid 函数的公式为：

\\[ f(y) = \frac{1}{1 + e^{-y}} \\]

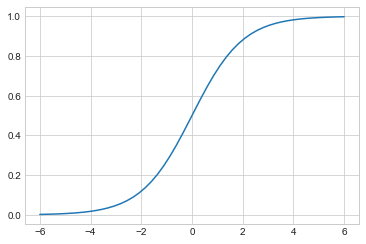
Sigmoid函数需要通过现有函数组合得到：

sigmoid = lambda x: 1.0 / (1.0 + np.exp(-x))

对于二分类问题，其预测分类的概率可以通过以下公式计算：

\\[ P = \frac{1}{1 + e^{-(k_0 + k_1x_1 + k_2x_2 + k_3x_3 + \dots)}} \\]

则分类为 0 的概率可表示为 \\( 1-P \\) 。

逻辑回归模型的本质就是计算各个属于各个分类的概率，并利用概率预测结果。

数学上使用极大似然估计法确定合适的系数 \\( k_i \\) 和截距项 \\( k_0 \\) 。

代码实现

Scikit-Learn 库中已经提供了逻辑回归模型。首先对原始数据做如下处理：

with open('titanic-survival.csv') as file:
    data = pd.read_csv(file).dropna()
X, Y = data[['Pclass', 'Gender', 'Age', 'Fare']], data['Survived']
X['Gender'] = X['Gender'].map({'male': 1, 'female': 0})

搭建逻辑回归模型的代码相比搭建线性回归模型区别只是使用的模型类不同：

from sklearn.linear_model import LogisticRegression
regr = LogisticRegression()
regr.fit(X, Y)
LogisticRegression()

同样可以利用搭建好的模型进行预测。简单对比几组预测值和真实值如下：

for i in range(105, 110):
    print(regr.predict([X.values[i]]), Y.values[i], end=' ** ')
[1] 1 ** [1] 1 ** [1] 1 ** [0] 0 ** [1] 1 **

可以看到预测的结果相当不错。

深入认识逻辑回归

逻辑回归更适合用于预测概率而不是直接划分具体类别。

通过 .predict_proba() 方法可以借助模型预测一些数据的概率：

y_proba = regr.predict_proba(X.values[87:92])
y_proba
array([[0.24235078, 0.75764922], [0.64814835, 0.35185165], [0.45878211, 0.54121789], [0.60972086, 0.39027914], [0.74556908, 0.25443092]])

前者是分类为 0 的概率，后者是分类为 1 的概率。一般将数据划分到概率更大的分类中。

模型计算出的特征变量系数和截距同样可以通过 .coef_ 和 .intercept_ 属性获得。

注意这是二分类模型下分类为 1 的系数和截距。可利用它们表达出具体的概率函数，计算分类为 1 的概率：

P = lambda X: 1/ (1 + np.exp(-(np.dot(X, regr.coef_.T) + regr.intercept_)))

对系数转置的目的是为了点乘运算。这与以上方式计算的概率是一致的。

除了二分类，逻辑回归还可以解决多分类问题，即 Y 值内不单单包含 0 和 1 ，还包含其它值（例如 -1 ）。

多分类问题下，计算得到的系数和截距是每一个分类的。

检验模型

使用训练集与测试集

模型搭建和使用前可以将数据划分为训练集数据和测试集数据。训练集用于训练数据和搭建模型，测试集用于检验训练模型的效果。其目的有：

通过如下代码可以将数据划分为训练集和测试集：

from sklearn.model_selection import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2)

这样，原始数据便被划分为 8:2 的训练集和测试集比例。

每次的划分都是随机的，如果要让两次使用相同的划分，需要指定 random_state 参数一致。

判断准确率

划分数据后，将训练集的数据用于搭建模型，并将得到的模型应用于测试集，对比所有的预测值和实际值，便能得到模型的准确率。

首先快速搭建一个逻辑回归模型：

model = LogisticRegression()
model.fit(X_train, Y_train)
LogisticRegression()

使用以下代码可以计算模型的预测准确度：

from sklearn.metrics import accuracy_score
accuracy_score(Y_test, model.predict(X_test))
0.7027027027027027

注意第一个参数是真实值，第二个参数是预测值。

还可以使用模型自带的 .score() 方法根据测试集直接计算：

model.score(X_test, Y_test)
0.7027027027027027

结果是一样的。

模型评估方法

对于二分类模型，主流的评估方法有ROC曲线和KS曲线两种。

ROC曲线

基本原理

以上预测的准确度看似不错，但是准确度可能只是恰好重合较多。考虑一个极端情况，即便预测所有的结果为 1 ，其准确率为：

accuracy_score(Y_test, np.ones(len(X_test)))
0.6216216216216216

因此实际上更关系下表的两个指标：

命中率（真正率） True Positive Rate(TPR) TPR = TP / (TP + FN)
假命中率 False Positive Rate(FPR) FPR = FP / (FP + TN)

其中 TF 、FP 、TN 、FN 的含义见下表，该表也被称为混淆矩阵：

1（预测真） 0（预测假） 合计
1（实际真） True Positive(TF) 正确肯定 False Negative(FN) 漏报 TP + FN
0（实际假） False Positive(FP) 虚报 True Negative(TN) 正确否定 FP + TN

总体来说，命中率需要计算所有实际为真（分类为1）中预测为真的比例，也称真正率或召回率；而假警报率计算的是所有实际为假（分类为0）中预测为假的比例，也称假正率。

再次列出公式如下：

\\[ \text{True Positive Rate (TPR)} = \frac{\text{True Positive (TP)}}{\text{True Positive (TP)} + \text{False Negative (FN)}}\\ \text{False Positive Rate (FPR)} = \frac{\text{False Positive (FP)}}{\text{False Positive (FP)} + \text{True Negative (TN)}} \\]

一个良好的模型应该拥有高命中率（TPR）和低假警报率（FRP），即尽可能找出属于该组的，但也要排除不属于该组的。这两个情况却不能同时保证。

ROC曲线代表不同阈值下命中率和假警报率，如下图：

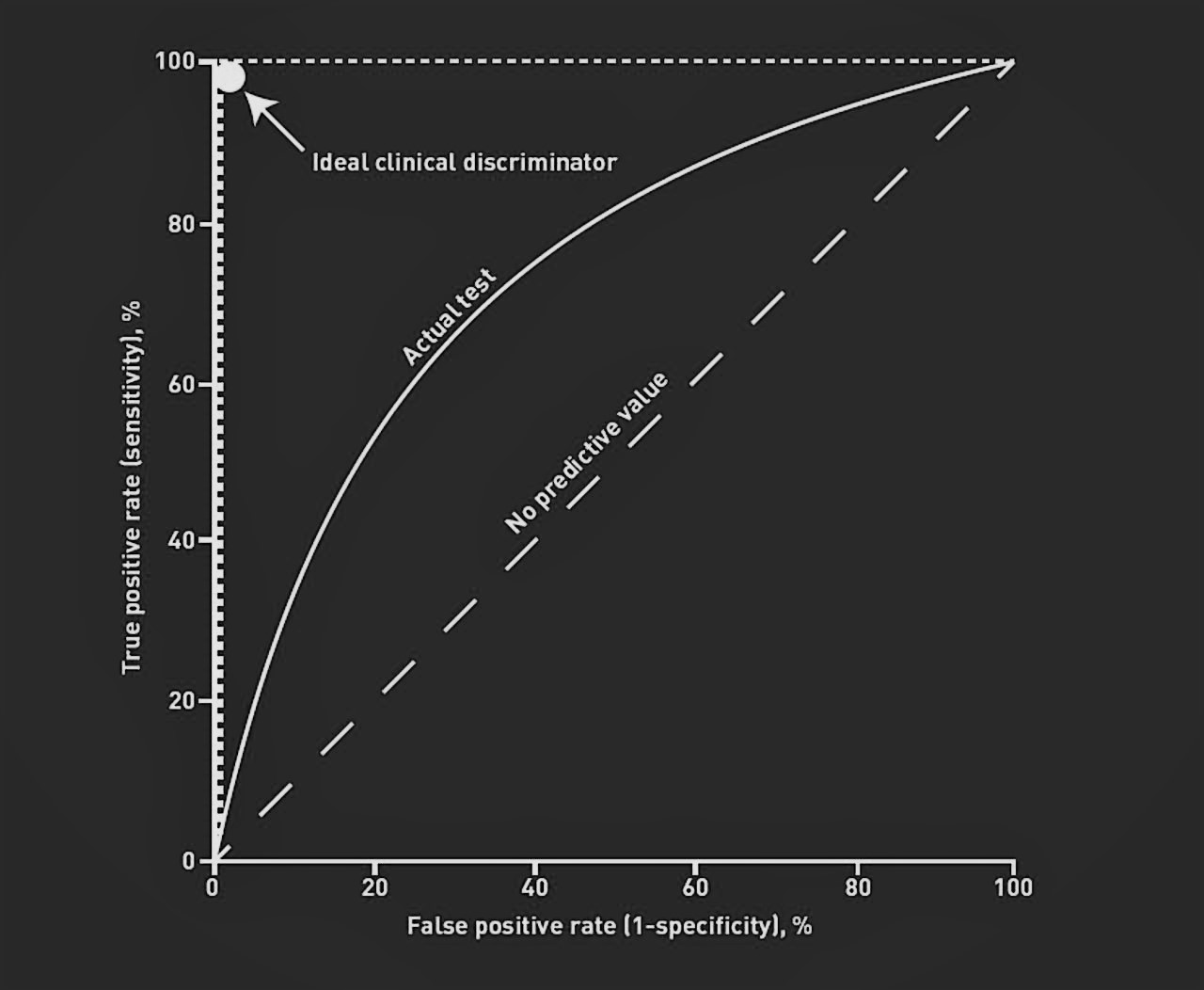
图片来源：https://www.displayr.com/what-is-a-roc-curve-how-to-interpret-it/

横坐标为假警报率(FPR)，纵坐标为命中率(TPR)。

一个完美的模型希望假警报率接近 0 ，命中率接近 1 ，即左上角顶点。一般的模型不可能达到该值，只能尽可能接近它，反应在图形上就是ROC曲线最接近左上角的一点，为模型的最优情况。

代码实现

首先，查看混淆矩阵的方法如下：

from sklearn.metrics import confusion_matrix
confusion_matrix(Y, model.predict(X))
array([[ 37, 23], [ 18, 105]], dtype=int64)

通过如下代码可以查看该数据的完整分析结果：

from sklearn.metrics import classification_report
print(classification_report(Y, model.predict(X)))
precision recall f1-score support 0 0.67 0.62 0.64 60 1 0.82 0.85 0.84 123 accuracy 0.78 183 macro avg 0.75 0.74 0.74 183 weighted avg 0.77 0.78 0.77 183

从中可以看出数据的召回率(recall)和整体准确度(accuracy)

除此之外，还有样本数(support)、精确度(precision)和 f1-score 。后两个数值的含义见下表：

名称 公式 含义
precision / 准确度 TP / (TP + FP) 预测为 1 类中实际为 1 类中的比例
f1-score 2TP / (2TP + FP + FN) 混合的度量，对不平衡类别比较有效

在数值上通常使用 AUC 值来衡量模型的好坏。AUC 值(Area Under Curve)即曲线下方的面积，取值范围为 \\( (0.5, 1) \\) ，通常达到 0.75 表示可以接受，0.85 表示非常不错。

通过如下代码可以求出不同阈值下的命中率(TPR)和假警报率(FPR)值，从而绘制ROC曲线：

from sklearn.metrics import roc_curve
FPR, TPR, thres = roc_curve(Y, regr.predict_proba(X)[:, 1])

注意，计算得到的概率包含两个分类的，这里只要用到其中一个。计算得到的结果还包含阈值(threshold)。

查看部分得到的计算值如下：

roc = pd.DataFrame({'threshold': threshold, 'FPR': FPR, 'TPR': TPR})
roc.head(4)
thresholdFPRTPR
01.9736890.0000000.000000
10.9736890.0023580.000000
20.9433120.0023580.075862
30.9420080.0047170.075862

第一个阈值超过 100% ，但它通常没有什么意义，仅保证没有任何记录被选中。其余阈值都是部分样本分类为 1 的概率。

已知不同阈值下的假警报率和命中率，可以通过以下代码绘制ROC曲线：

plt.plot(FPR, TPR)
plt.title('ROC curve'); plt.xlabel('FPR'); plt.ylabel('TPR')
plt.plot()

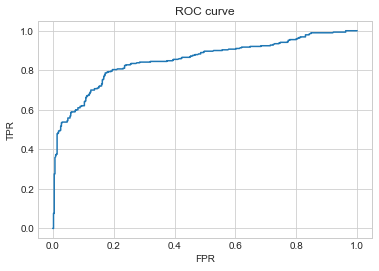
通过如下代码可以求出模型的AUC值：

from sklearn.metrics import roc_auc_score
roc_auc_score(Y_test, regr.predict_proba(X_test)[:, 1])
0.8144499178981939

其参数与求 ROC 曲线的函数是类似的。使用测试集获得的 AUC 值超过了 0.8 ，说明模型预测效果还不错。

KS曲线的基本原理

KS 曲线的本质也是关注命中率(TPR)和假警报率(FPR)，但该曲线将阈值作为横坐标，命中率(TPR)和假警报率(FPR)之差作为纵坐标，如下图所示：

书中原图

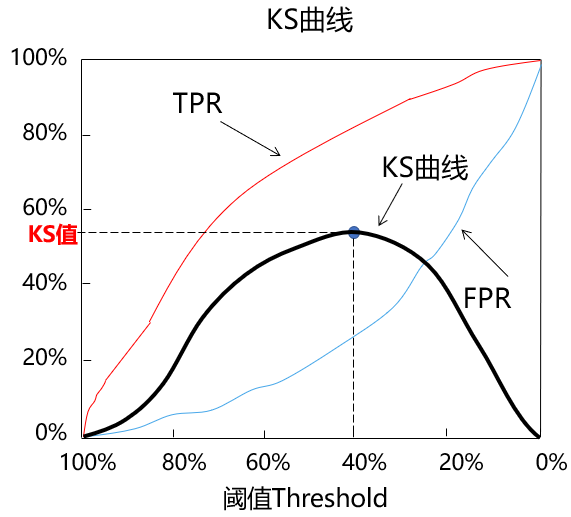
KS 曲线使用 KS 值来衡量模型预测效果，计算公式为：

\\[ \text{KS} = max(\text{TPR} - \text{FPR}) \\]

即曲线的峰值。不同 KS 值一般说明的规律如下：

通过以下代码绘制 KS 曲线：

plt.plot(threshold[1:], TPR[1:])
plt.plot(threshold[1:], FPR[1:])
plt.plot(threshold[1:], TPR[1:] - FPR[1:])
plt.xlabel('threshold')
plt.legend(['TPR', 'FPR', 'TPR-FPR'])
plt.gca().invert_xaxis()
plt.show()

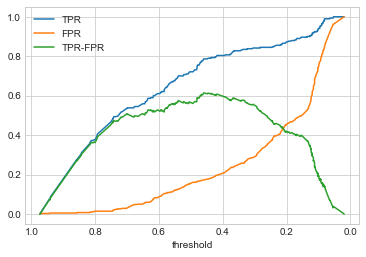
注意绘制时需要反转X轴。

通过如下代码可以求出KS值，并得出此时对应的阈值：

ks = pd.DataFrame({'threshold': threshold, 'TPR': TPR,
                   'FPR': FPR, 'TPR-FPR': TPR - FPR})
ks[ks['TPR-FPR'] == max(TPR - FPR)]
thresholdTPRFPRTPR-FPR
970.4598130.7862070.172170.614037

则此时阈值为 0.46 ，KS 值为 0.61 ，模型的预测能力非常不错。