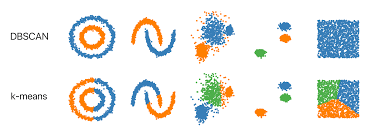数据聚类与分群分析
非监督式学习的数据集只有特征变量,而没有目标变量,需要对已有数据建模并根据性质分组。
KMeans算法
算法原理
KMeans算法 是一种常用的聚类算法,其中 K 代表数据,Means 代表每个类别内样本的均值。
KMeans算法以距离作为样本间相似度的度量标准,将距离相近的样本分配至同一个类别。KMeans算法通常采用欧氏距离来度量各样本间的距离。
KMeans算法的核心思想是先随机取几个中心点,计算每个样本到各自中心点的距离,并将样本分配给最近的中心点代表的类别;一次迭代完成后,根据聚类结果,更新中心点,然后重复之前的操作再次迭代,直到前后两次分类结果没有差别。
下图展示了KMeans聚类的原理:
图片来源: https://www.learnbymarketing.com/methods/k-means-clustering/
代码实现
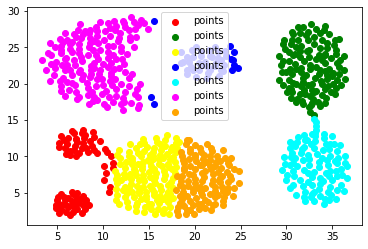
首先读取一些数据,并以散点图的形式粗略检查:
plt . scatter ( points . values [:, 0 ], points . values [:, 1 ],
c = ' magenta ' , marker = ' o ' , label = ' points ' )
plt . legend ()
plt . show ()
可以直接使用 Scikit-Learn 提供的工具完成KMeans聚类:
from sklearn . cluster import KMeans
kms = KMeans ( n_clusters = 7 )
kms . fit ( points )
KMeans(n_clusters=7)
这里,参数 n_clusters 即 K 值,表示样本聚成的类数。检查散点图发现,所有的点大致可以聚成 7 类。
可以使用 kms.labels_ 属性获取聚类结果,例如以下以散点图的形式表现出来:
colors = [ ' red ' , ' green ' , ' yellow ' , ' blue ' , ' cyan ' , ' magenta ' , ' orange ' ]
for i , color in enumerate ( colors ):
plt . scatter ( points . values [ kms . labels_ == i ][:, 0 ],
points . values [ kms . labels_ == i ][:, 1 ],
c = color , marker = ' o ' , label = ' points ' )
plt . legend ()
plt . show ()
结果整体来说划分良好。
DBSCAN算法
算法原理
DBSCAN算法全称 Densiity-Based Spatial Clustering of Applications with Noise ,是一种以密度为基础的空间聚类算法,可以用密度的概念剔除不属于任一类别的噪点。
该算法将簇定义为密度相连的点的最大集合,将具有足够密度的区域划分为簇,并可以发现任意形状的簇。
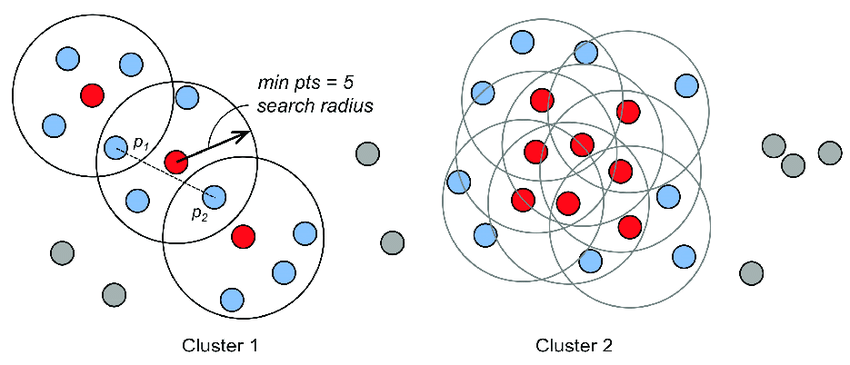
DBSCAN算法的基本步骤为:先随机选取一个点,以该样本点为圆心,按照设定的半径作圆。如果圆内的样本数大于等于设定的阈值,则将这些样本归为一类。接着选定圆内的其它样本点,继续作圆;如果某个圆内的样本数小于阈值,则放弃该圆的绘制。不断重复以上步骤,直到没有可画的圆为止,并将这些圆内的样本点归为一簇。
下图展示了该算法的思路:
引用自:Difrancesco, Paul-Mark & Bonneau, David & Hutchinson, D.. (2020). The Implications of M3C2 Projection Diameter on 3D Semi-Automated Rockfall Extraction from Sequential Terrestrial Laser Scanning Point Clouds. Remote Sensing. 12. 1885. 10.3390/rs12111885.
可以借助可视化网站 https://www.naftaliharris.com/blog/visualizing-dbscan-clustering/ 交互式查看DBSCAN算法聚类的过程。
代码实现
DBSCAN算法的实现与KMeans算法实现高度相似:
from sklearn . cluster import DBSCAN
dbs = DBSCAN ( eps = 1.5 )
dbs . fit ( points )
DBSCAN(eps=1.5)
下面以散点图的形式表现了聚类的结果:
colors = [ ' red ' , ' green ' , ' yellow ' , ' blue ' , ' cyan ' , ' magenta ' , ' orange ' ]
for i , color in enumerate ( colors ):
plt . scatter ( points . values [ dbs . labels_ == i ][:, 0 ],
points . values [ dbs . labels_ == i ][:, 1 ],
c = color , marker = ' o ' , label = ' points ' )
plt . legend ()
plt . show ()
以上使用KMeans和DBSCAN算法对同一组数据聚类,对比结果可以发现:DBSCAN算法在聚类时可以发现任意形状的簇将其聚为一类,而KMeans算法只是机械地将距离近的数据归到同一组。
下图对比了KMeans算法与DBSCAN算法的聚类结果:
图片来源:未知
下表对比了两种算法:
算法名称 优点 缺点
KMeans算法
适用于常规数据集
适用于高维数据的聚类
适用于密度会发生变化的数据聚类
需要事先知道K值
初始中心点的选择会在较大程度上影响聚类结果
难以发现任意形状的簇
DBSCAN算法
不需要事先知道K值
可以发现任意形状的簇
可以识别出噪点(游离点)
初始中心点选择不影响聚类结果
不适用于高位数据的聚类
不适用于密度会发生变化的数据聚类
参数难以确实最优值
示例:新闻聚类分群
代码实现
本节使用聚类来将新闻分群。
以下代码是一个精简的百度新闻爬虫,可以按关键词获取某一页的所有新闻项信息:
import re
import requests
import pandas as pd
headers = {
' User-Agent ' : ' Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/98.0.4758.102 Safari/537.36 '
}
def baidu ( keyword , page ):
num = ( page - 1 ) * 10
url = f 'https://www.baidu.com/s?tn=news&rtt=4&bsst=1&cl=2&wd= { keyword } &pn= { num } '
response = requests . get ( url , headers = headers ). text
href = re . findall ( r '<h3 class="news-title_1YtI1"><a href="(. *? )"' , response )
title = re . findall ( r '<h3 class="news-title_1YtI1">. *? >(. *? )</a>' , response , re . S )
for i , t in enumerate ( title ): title [ i ] = re . sub ( r '<. *? >' , '' , t )
return pd . DataFrame ({ ' 关键词 ' : keyword , ' 标题 ' : title , ' 网址 ' : href })
df = pd . DataFrame ()
keywords = [ ' Python ' , ' 大数据 ' , ' 机器学习 ' , ' 人工智能 ' , ' 动漫 ' , ' 服务器 ' ]
for k in keywords :
for i in range ( 10 ):
df = df . append ( baidu ( k , i + 1 ))
df . to_excel ( ' 新闻.xlsx ' )
在使用 Pandas 提供的 Excel 读写功能前,还需要安装 openpyxl 库。
使用以下代码读取爬虫生成的 Excel 表:
news = pd . read_excel ( ' 新闻.xlsx ' )
由于爬虫获取的是中文结果,因此这里使用 jieba 库来分词:
import jieba
words = [ ' ' . join ( jieba . cut ( row [ ' 标题 ' ])) for i , row in news . iterrows ()]
此时已经将新闻标题分词完毕。接下来需要将这些文本进行向量化 处理并建立词频矩阵。这一步的目的是将文本类型的数据转换为数值类型的数据,以便构造特征变量及训练模型。
使用 Scikit-Learn 库可以方便地执行文本向量化处理:
from sklearn . feature_extraction . text import CountVectorizer
vect = CountVectorizer ()
X = vect . fit_transform ( words )
jieba 分词结果构成了新闻标题的词袋,向量化处理时会自动对词袋里的词编号。
通过以下代码可以获取词袋的内容及编号(得到的结果是一个字典,这里仅取其中的部分值):
print ( list ( vect . vocabulary_ . items ())[: 10 ])
[('python', 184), ('保留', 446), ('两位', 291), ('小数', 917), ('什么', 387), ('基础教程', 772), ('超全', 1846), ('获取', 1741), ('某一', 1328), ('日期', 1239)]
向量化时,CountVectorizer 类还会自动过滤一个字的词,这样优点是会过滤掉大多数无意义的词,缺点是极少数有意义的词也可能被过滤。
可以通过以下代码构造用于学习的 DataFrame 对象:
word_freq = pd . DataFrame ( X . toarray (), columns = vect . get_feature_names ())
.toarray() 方法返回的数组包括一系列的 0 和 1 ,表示是否有词袋对应编号的词;.get_feature_names() 方法返回的是按编号顺序排列的词,两者结合正好能得到一一对应的表。
下面使用KMeans算法对得到的结果聚类,DBSCAN聚类方法类似:
from sklearn . cluster import KMeans
kms = KMeans ( n_clusters = 6 , random_state = 42 )
groups = kms . fit_predict ( word_freq )
以下代码查看分类为 1 的数据中分词后的新闻标题的前 4 项:
print ( np . array ( words )[ groups == 1 ][: 4 ])
['「 20 」 数据 可视化 + 爬虫 : 基于 Echarts + Python + Pandas 大屏 范例'
'海洋 数据 产生 量 爆发式 增长 海洋 科学 大 数据 行业 前景 广阔'
'看 ! “ 大 数据 ” 背后 的 中国 “ 她 力量 ”'
'“ 她 ” 画像 | 2022 金融 圈 女性 大 数据 : A股 女性 基金 经理 777 人 、 董事长 ...']
从结果中可以看出,这个分类应该是与“大数据”相关。
结果分析
这里简单检查一下分类的结果:
from collections import Counter
print ( Counter ( groups ))
Counter({3: 216, 1: 106, 2: 88, 0: 81, 5: 67, 4: 1})
在爬取数据时,是以 6 个关键字总共爬取559条数据,每个关键字对应的数据量相近。但是KMeans聚类结果每个组数据量相差甚远。
事实上,如果采用DBSCAN算法聚类,聚类的结果更差,原因主要是太多游离点使分组过多。
造成KMeans聚类差距的主要原因是新闻标题长短不一,在中文分词及文本向量化后,长标题和短标题的距离就较远,因此容易被划分到不同的类中。
考虑以下词频矩阵:
something result good bad
0 1 1 0 1
1 2 2 2 0
2 3 3 0 2
计算得到的 0 和 1 的欧氏距离为 \\( \sqrt 7 \\) ,而 0 和 2 的欧氏距离为 \\( \sqrt 9 \\) ,然而直观感受 0 和 2 才是最接近的。
这种因为文本的长短造成的预测不精确可以通过余弦相似度来解决。余项相似度是根据向量夹角来判断相似度。
结果优化:余弦相似度
数学原理
在向量空间中可以采用两个向量夹角的余弦值 \\( \cos \theta \\) 来表示它们的相似度,称为余弦相似度 。余弦值越大,说明向量夹角越小,向量越相似。
向量的余弦值由以下公式给出:
\\[
\begin{split}
\cos \theta &= \frac{\boldsymbol{a} \cdot \boldsymbol{b}}{|\boldsymbol{a}||\boldsymbol{b}|} \\
&= \frac{x_1x_2+y_1y_2}{\sqrt{x_1^2+y_1^2} \cdot \sqrt{x_2^2+y_2^2}}
\end{split}
\\]
对于之前的词频矩阵,计算得到的 0 和 1 的余弦相似度为 \\( 0.667 \\) ,而 0 和 2 的余弦相似度为 \\( 0.984 \\) ,该结果与实际相符。
代码实现
Scikit-Learn 提供了余弦相似度处理的工具,处理得到的结果类似变量的关联系数:
from sklearn . metrics . pairwise import cosine_similarity
X_cossim = cosine_similarity ( word_freq )
将得到的结果使用KMeans聚类如下:
kms = KMeans ( n_clusters = 6 , random_state = 42 )
groups = kms . fit_predict ( X_cossim )
print ( Counter ( groups ))
Counter({5: 152, 0: 103, 1: 88, 2: 86, 4: 65, 3: 65})
尽管还存在误分类,但是此时的结果已经比之前好很多了。