机器学习入门笔记01

线性回归模型

系列文章

线性回归模型

一元线性回归

线性回归模型是利用线性拟合的方式，寻找样本点背后的回归曲线（趋势线），再利用回归曲线进行简单的分析。

线性回归根据特征变量（自变量）来预测反应变量（因变量）。根据特征变量的个数可将线性回归模型分为一元线性回归和多元线性回归。

数学原理

一元线性回归模型可以表示为如下公式：

\\[ y = ax + b \\]

其中 \\( y \\) 为因变量，\\( x \\)为自变量，\\( a \\) 为回归系数，\\( b \\) 为截距。

实际值 \\( y^{(i)} \\) 与预测值 \\( \hat y^{(i)} \\) 之间的接近程度可以用它们的残差平方和（即差值的平方）来衡量：

\\[ \sum (y^{(i)} - \hat y^{(i)}) ^ 2 \\]

上式可以变形为：

\\[ \sum (y^{(i)} - (ax^{(i)} + b)) ^ 2 \\]

通过对上式求导并令导数为0，可得残差平方和最小，即拟合最优时的回归系数 \\( a \\) 和截距 \\( b \\) 。以上方法称为最小二乘法。

代码实现。

通过Python的 Scikit-Learn 库可以直接调用一元线性回归模型。该库可以直接通过 pip 命令安装：

(sci) PS D:\MachineLearning\demo> pip install sklearn

在Jupyter Notebook中，首先导入需要的库并加载数据集：

import sklearn
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
with open('linear-regression-train.csv', 'r') as f:
    data = pd.read_csv(f)
    X, Y = data['x'], data['y']
%matplotlib inline

将数据集绘制成散点图，如下所示：

plt.scatter(X, Y)
plt.show()

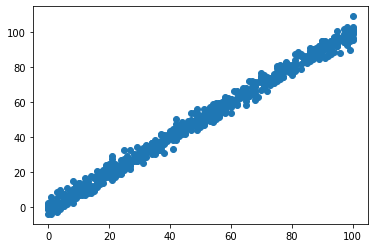
如果要将这些数据运用线性回归处理，自变量中的每个元素要写成一个数组形式，这是因为在多元回归中一个因变量可能对应多个自变量。

可以使用以下代码将自变量中的每一个元素变成一个单元素数组：

X_train = X.values[:, np.newaxis]
X_train[0]
array([24], dtype=int64)

利用原始数据，使用Scikit-Learn库只需要3行代码即可得到线性回归模型：

from sklearn.linear_model import LinearRegression
regr = LinearRegression()
regr.fit(X_train, Y)
LinearRegression()

使用 .fit() 方法就可以搭建一个线性回归模型。利用搭建好的模型，可以使用 .predict() 方法可以预测因变量的值：

regr.predict([[200]])
array([200.03549408])

注意自变量还需要写成二维数组的模式。如果要预测多个自变量，只需要多添加几行即可。

可以将搭建完成的模型以可视化的形式展示出来：

plt.scatter(X, Y)
plt.plot(X, regr.predict(X_train), color='yellow')
plt.show()

可以看到 regr.predict() 代表的就是回归函数。

还可以通过 coef_ 和 intercept_ 属性得到模型计算的趋势线系数和截距：

print('a: ', regr.coef_)
print('b: ', regr.intercept_)
a: [1.00077825] b: -0.12015553181321792

计算依据的原理就是最小二乘法。

模型优化

有时候趋势线是曲线，此时可以使用一元多次线性回归模型。其形式可表现为如下的公式：

\\[ y = a_nx^n + a_{n-1}x^{n-1} + \dots + a_2x^2 + a_1x + a_0 \\]

对于多次线性回归模型，引入数据的方式是一致的：

with open('polynomial-regression-train.csv', 'r') as f:
    data = pd.read_csv(f)
X, Y = data['X'], data['Y']
X_train = X.values[:, np.newaxis]

但是在使用数据前，还需要对其进行一些 预处理 ，生成多次项数据：

from sklearn.preprocessing import PolynomialFeatures
X_poly = PolynomialFeatures(degree=3).fit_transform(X_train)

实际上，这一步的目的就是将原有的每条数据 \\( [ \, x \, ] \\) 变成形如 \\( [ \, 1, \, x, \, x^2, \dots, x^n \, ] \\) 形式。其中第一列 1 为常数项，它的值对分析结果没有影响。

这样生成的二次项数据可以直接代入线性模型获得一元多次线性回归模型：

regr_poly = LinearRegression()
regr_poly.fit(X_poly, Y)
LinearRegression()

绘制曲线图来查看得到的预测曲线效果：

plt.scatter(X, Y)
plt.plot(X, regr_poly.predict(X_poly), color='red')
plt.show()

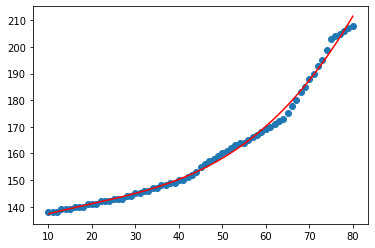
注意 .predict() 方法的参数形状要匹配。

线性回归模型评估

线性回归的模型评估主要以3个值进行作为评价标准：R-square（即 \\( R^2 \\) ）、Adj. R-square（即 \\( \text{Adjusted}\, R^2 \\)） 和 \\( P \\) 值

数学原理

R-square

设 \\( Y_\text{i} \\) 为实际值，\\( Y_{\text{fitted}} \\) 为预测值，\\( Y_{\text{mean}} \\) 为所有散点的平均值，则数据的整体平方和 \\( \text{TSS} \\) 、残差平方和 \\( \text{RSS} \\) 以及解释平方和 \\( \text{ESS} \\) 可以根据以下公式计算：

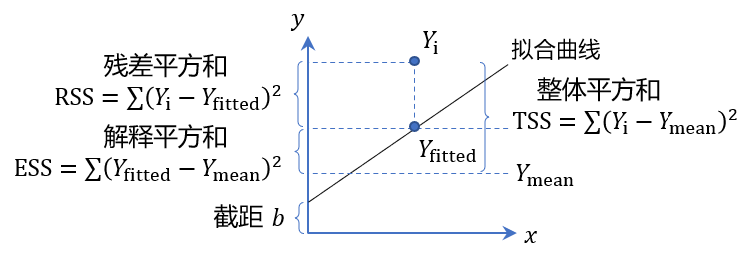
对 \\( R^2 \\) ，有如下计算公式：

\\[ R^2 = 1 - \frac{\text{RSS}}{\text{TSS}} \\]

对于线性回归模型，如果拟合度较高，则残差平方和 \\( \text{RSS} \\) 需要尽可能小，即 \\( R^2 \\) 尽可能大。当 \\( R^2 \\) 趋向 1 时，\\( \text{RSS} \\) 趋向 0 ，即基本所有点落在回归直线上。

不能为了盲目增加 \\( R^2 \\) 而增加回归曲线的次数，否则可能发生过拟合，这样得出的数据不具有推广性。与之相对应的概念是欠拟合，模型没有捕捉到数据的特征，不能拟合数据。

Adj. R-square

Adj. R-square 是改进的 R-square ，目的是防止选取特征变量过多导致 R-square 值虚高。

Adj. R-square 在 R-square 的基础上考虑了特征变量的数量这一因素，其公式为：

\\[ \bar{R^2} = 1 - \frac{(1 - R^2)(n - 1)}{n - k - 1} \\]

其中 \\( n \\) 为样本数量，\\( k \\) 为特征变量数量。因此选择的特征变量越多，对 Adj. R-square 影响便越大。

P值

\\( P \\) 值通过假设特征变量与目标变量无显著相关性，所得到的样本观察结果或更极端结果出现的概率：若概率越大，则 \\( P \\) 值越大，原假设为真的可能性便越大；若 \\( P \\) 值越小，说明显著相关性越大。

通常以 \\( P \\) 值 0.05 为特征变量与目标变量是否有显著相关性的阈值。

代码实现

statsmodels 是一个分析统计模型的Python库。可以通过 pip 直接安装：

(sci) PS D:\MachineLearning\demo> pip install statsmodels

利用该库，只需通过以下几行代码便可以分析搭建回归模型的各种数据信息：

import statsmodels.api as sm
est = sm.OLS(Y, sm.add_constant(X_train)).fit()
est.summary()
OLS Regression Results
Dep. Variable:Y R-squared: 0.897
Model:OLS Adj. R-squared: 0.896
Method:Least Squares F-statistic: 603.2
Date:Mon, 14 Feb 2022 Prob (F-statistic): 7.88e-36
Time: 17:04:35 Log-Likelihood: -235.06
No. Observations: 71 AIC: 474.1
Df Residuals: 69 BIC: 478.6
Df Model: 1
Covariance Type: nonrobust
coef std err t P>|t| [0.025 0.975]
const 117.8260 1.926 61.176 0.000 113.984 121.668
x1 0.9566 0.039 24.559 0.000 0.879 1.034
Omnibus: 9.822 Durbin-Watson: 0.019
Prob(Omnibus): 0.007 Jarque-Bera (JB): 8.140
Skew: 0.729 Prob(JB): 0.0171
Kurtosis: 2.208 Cond. No. 119.
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

注意，通过 sm.add_constant() 函数是为了给原来的特征变量 X 添加常数项，即公式 \\( y=ax+b \\) 中的截距 \\( b \\) 。

注意结果表格中用红色强调的部分。左下角就是常数项和特征变量前的系数，即截距 \\( b \\) 和斜率 \\( a \\) 。

评估模型通常需要关心表中的 R-square 、Adj. R-square 和 \\( P \\) 值。以上搭建线性模型的 R-square 和 Adj. R-square 都达到了 0.89 以上，说明模型的线性拟合程度较好。

类似地还可以搭建一元多次线性回归模型并对它分析，相关的代码如下：

from sklearn.preprocessing import PolynomialFeatures
X_poly = PolynomialFeatures(degree=5).fit_transform(X_train)
regr_poly = LinearRegression()
regr_poly.fit(X_poly, Y)

est = sm.OLS(Y, sm.add_constant(X_poly)).fit()  # get analyse result
from re import split
summary = split(r'\n|,', est.summary().as_csv())
print('R-square:      ', summary[4].strip())
print('Adj. R-square: ', summary[8].strip())
R-square: 0.996 Adj. R-square: 0.996

Scikit-Learn库自带的自带的函数就可以计算获取 R-square 值，方法如下：

from sklearn.metrics import r2_score
r2_score(Y, regr.predict(X_train))
0.9906694842900379

这里利用的是之前一元线性回归的数据。

多元线性回归

多元线性回归是推广到多个变量的线性回归模型，可以考虑多个变量对目标因素的影响。

多元线性回归可以表示为如下所示的公式：

\\[ y = k_0 + k_1x_1 + k_2x_2 + \dots + k_nx_n + \dots \\]

其中 \\( x_i \\) 为不同的特征变量，\\( k_i \\) 为这些特征变量前的系数，\\( k_0 \\) 为常数项。

多元线性回归模型的的原理也是取合适系数，使残差平方和

\\[ \sum (y^{(i)} - \hat y^{(i)})^2 \\]

最小。数学上主要通过最小二乘法和梯度下降法来计算合适的系数。

多元线性回归的核心代码和一元线性回归的代码是一致的，只不过自变量中的每项都包含多个特征变量信息。

以下列出了完整的代码，主要步骤包含获取数据、建立模型、分析模型和打印结果：

with open('multiple-linear-regression.csv', 'r') as f:
    data = pd.read_csv(f)
X_multi, Y = data.iloc[:, :-1], data['Profit']   # fetch data

regr_multi = LinearRegression()                  # build model
regr.fit(X_multi, Y)

est = sm.OLS(Y, sm.add_constant(X_multi)).fit()  # analyse

summary = split(r'\n|,', est.summary().as_csv())
print('R-square:      ', summary[4].strip())
print('Adj. R-square: ', summary[8].strip())
print('\n'.join([f'{summary[52 + i*7].strip():15}'
                 f'{summary[53 + i*7].strip():>10}    '              # co-ef
                 f'{summary[56 + i*7].strip()}' for i in range(4)])) # P-value
R-square: 0.951 Adj. R-square: 0.946 R&D Spend 0.8060 0.000 Administration -0.0270 0.604 Marketing Spend 0.0270 0.116 State 118.5147 0.943

模型整体拟合效果很好。观察各自变量的 \\( P \\) 值可以得出，利润与研发费用的相关性非常强，与营销支出的相关性较强，与选址几乎没有关系。